在数据科学和机器学习限制,构建可靠且隆重的模子是进行准确展望和得回有价值视力的关键。然而当模子中的变量启动呈现出高度联系性时,就会出现一个常见但容易被疏远的问题 —— 多重共线性。多重共线性是指两个或多个展望变量之间存在强联系性,导致模子难以差别它们对方针变量的孝顺。如果疏远多重共线性,它会扭曲模子的效用,导致统统的可靠性着落,进而影响决议的准确性。本文将深远探讨多重共线性的实质,陈诉其要紧性,并提供有用措置多重共线性的方法,同期幸免数据科学家常犯的罗网。

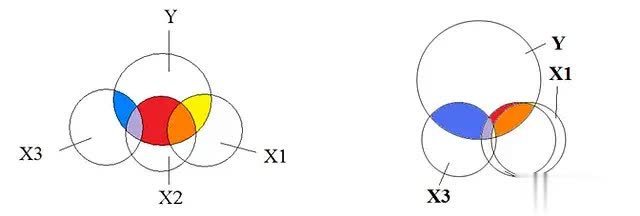
多重共线性是指数据贴近两个或多个自变量(展望变量)之间存在热烈的线性联系性。简而言之,这些自变量包含了近似的信息,而不是提供展望因变量(方针变量)所需的惟一信息,使得模子难以细目每个自变量的individual孝顺。

在总结分析中,自变量(independent variable)是影响效用的因素,而因变量(dependent variable)是咱们试图展望的效用。举个例子,在房价展望模子中,房屋面积、卧室数目和地舆位置等因素被视为自变量,而房价动作因变量,取决于这些自变量的变化。

为了充分分解多重共线性的影响,咱们需要先了解线性总结的一些学问。

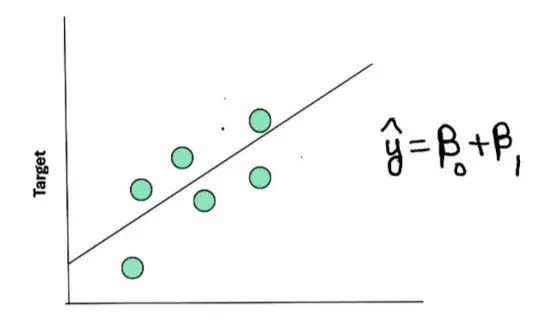
假定咱们有一组用绿点示意的数据,咱们但愿通过这些点拟合一条直线来进行展望。穿过这些点的直线被称为总结线,它对数据进行了玄虚和总结。

在这个简单的例子中,方针变量(房价)是因变量,咱们使用一个自变量(如房屋面积)来展望它。一个简单线性总结的方程不错示意为:

ŷ = β₀ + β₁X

其中:

ŷ 示意展望值(总结线上的一个点)。

X 示意自变量的值。

β₀ 示意截距(总结线与y轴的交点)。

β₁ 示意斜率(总结线的斜率)。

施行数据点与展望值(ŷ)之间的互异被称为残差(residual)或过失(error):

残差 = yᵢ - ŷᵢ

其中:

yᵢ 示意第i个不雅测值的施行值。

ŷᵢ 示意第i个不雅测值的展望值。

线性总结的方针是通过最小化残差平常和来找到最好拟合直线,使得展望值与施行值之间的互异最小。

在多元线性总结中,咱们使用多个自变量来展望因变量,其方程不错示意为:

ŷ = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ

其中:

X₁, X₂, …, Xₚ 示意不同的自变量(如房屋面积、卧室数目、地舆位置等)。

β₁, β₂, …, βₚ 示意各个自变量对应的总结统统。

咱们但愿每个自变量对方针变量有其独到的孝顺。诚然因变量与自变量之间的联系性是咱们所渴望的,但自变量之间的联系性却是咱们需要幸免的。举例,咱们不但愿出现以下情况:

X₂ = β₀ + β₁X₁

这便是多重共线性的发达 —— 自变量之间发达出类似因变量的线性关系,给模子的教练和推断带来了玷辱和不细目性。

让咱们通过一个简单的例子来分解多重共线性的影响。有计划以下用于展望方针变量ŷ的方程:

ŷ = 10 + 2X₁ + 5X₂

假定 X₁ 和 X₂ 之间存在强联系性,咱们不错将它们的关系示意为:

X₁ = X₂ + 1

那么,原始方程不错悠扬为以下两种面容:

ŷ = 12 + 0X₁ + 9X₂

ŷ = 7.5 + 4.5X₁ + 0X₂

当前,咱们有三个不同的方程来展望 ŷ ,这导致模子产生了玷辱:

截距项(intercept)应该是10、12也曾7.5?

X₁ 和 X₂ 的统统(coefficients)应该若何细目?

由于 X₁ 和 X₂ 之间的联系性,总结统统变得不牢固和不可靠。跟着多重共线性进程的加多,模子中的统统揣度会出现更大的波动,导致模子的不牢固和不可靠。这种不细目性使得咱们难以证实自变量和因变量之间的实在关系,这便是为什么有用措置多重共线性至关要紧。

措置多重共线性有多种有用的方法。以下是一些常用的本事:

从联系变量对中移除一个特征: 如果两个变量高度联系,不错有计划移除其中一个,以减少冗余信息。

查验方差延长因子(VIF): 识别具有高VIF值的特征,这标明存在多重共线性。移除高VIF特征有助于提升模子的牢固性。

使用主因素分析(PCA)进行数据调遣: PCA通过创建原始变量的线性组合来缩短数据维度,从而甩掉多重共线性。

诓骗岭总结(Ridge Regression)或Lasso总结: 这些正则化本事通过收缩总结统统来缩小多重共线性的影响。岭总结通过最小化统统的L2范数来达成,而Lasso总结则通过最小化统统的L1范数,不错将一些统统压缩为零。

盲目移除联系特征: 这种方法在只须少数特征联系的情况下是可行的,但如果存在多数联系特征,则可能不太实用。

过度依赖PCA: 尽管PCA在缩小多重共线性方面极度有用,但更生成的变量可证实性较差,这使得向非本事利益联系者证实效用变得更具挑战性。

对岭总结和Lasso总结的歪曲: 诚然这些方法不错缩小多重共线性的影响,但它们主如若正则化本事。它们并不成宽裕"颐养"多重共线性,而是通过调整统统来匡助纪律其影响。

有计划到这些局限性,咱们连接会将 方差延长因子(VIF) 动作识别和措置多重共线性的最有用器具之一。VIF不错匡助咱们细目导致多重共线性的特征,从而作念出贤慧的决议,在保捏模子可证实性的同期提升其牢固性。

方差延长因子(VIF)是一种统计度量,用于检测总结模子中是否存在多重共线性。它量化了由于自变量之间的多重共线性而导致的总结统统方差的延前程程。VIF告诉咱们其他自变量对特定展望变量方差的影响进程。

为了更好地分解VIF,让咱们先追想一下总结分析中的一个关键意见:决定统统(coefficient of determination),也称为R²。R²用于评估总结模子对数据的拟合优度。举例,R² = 0.9意味着方针变量(ŷ)中90%的变异不错由模子中的自变量证实。

VIF通过以下门径匡助咱们识别和甩掉模子中的多重共线性:

门径1: 对每个自变量成立一个线性总结模子,使用数据贴近的其他自变量动作展望变量。这意味着咱们不是径直展望方针变量(ŷ),而是尝试用其他自变量来证实每个自变量。

举例:

X₁ = αX₂ + αX₃ + … + αXₚ

X₂ = θX₁ + θX₃ + … + θXₚ

X₃ = δX₁ + δX₂ + … + δXₚ

在VIF的操办流程中,咱们为每个自变量拟合一个线性总结模子,使用数据贴近其余的自变量动作展望变量。

门径2: 关于每个线性总结模子,咱们操办决定统统R²。这给出了每个自变量的R²值(记为R²ᵢ),示意其他自变量大要证实该自变量变异性的进程。

门径3: 使用以下公式操办每个自变量的VIF:

VIFᵢ = 1 / (1 - R²ᵢ)

这个公式标明,当R²ᵢ加多时,VIF也会随之加多。举例:

如果R²ᵢ = 1,则VIFᵢ = ∞(宽裕多重共线性)。

如果R²ᵢ = 0.9,则VIFᵢ = 10。

如果R²ᵢ = 0.8,则VIFᵢ = 5。

VIF值较高示意该自变量与其他自变量高度共线,这可能会扭曲总结统统的揣度。

基于VIF的特征取舍连接以迭代的表情进行。这意味着咱们每次移除一个具有高VIF值的特征,然后再行操办剩余特征的VIF值。重复这个流程,直到扫数特征的VIF值皆低于设定的阈值(连接为5或10)。

由于移除一个特征会影响其他特征之间的多重共线性,因此在每次移除后再行操办VIF值很要紧,以确保模子缓缓变得愈加牢固和可靠。

以下是一段使用Python达成VIF操办和基于VIF的特征取舍的代码示例:

from statsmodels.stats.outliers_influence import variance_inflation_factorfrom statsmodels.tools.tools import add_constantdef calculate_vif(X): """ 操办给定自变量矩阵X的方差延长因子(VIF) """ # 添加常数项 X = add_constant(X) # 操办每个特征的VIF vif = pd.Series([variance_inflation_factor(X.values, i) for i in range(X.shape[1])], index=X.columns) return vifdef vif_feature_selection(X, threshold=5): """ 基于VIF的特征取舍 """ vif = calculate_vif(X) while vif.max() > threshold: # 移除具有最大VIF值的特征 feature_to_remove = vif.idxmax() X = X.drop(columns=[feature_to_remove]) # 再行操办VIF vif = calculate_vif(X) return X# 使用示例selected_features = vif_feature_selection(X)

在这个示例中,咱们界说了两个函数:

calculate_vif(X):操办给定自变量矩阵X的VIF值。它领先为X添加一个常数项,然后使用variance_inflation_factor()函数操办每个特征的VIF。

vif_feature_selection(X, threshold=5):基于VIF进行特征取舍。它重复操办VIF并移除具有最大VIF值的特征,直到扫数特征的VIF值皆低于给定的阈值(默许为5)。

这段代码演示了若何使用VIF进行多重共线性检测和特征取舍的完好意思流程。将其诓骗于我方的数据集,以识别和措置多重共线性问题。

分解和措置多重共线性关于构建可靠和可证实的总结模子至关要紧。当自变量之间存在高度联系性时,可能导致总结统统揣度不牢固、规范过失延长以及模子展望不可靠。通过使用移除联系特征、主因素分析(PCA)、岭总结或Lasso总结等本事,咱们不错有用地缩小多重共线性的影响。

在繁多措置多重共线性的方法中,方差延长因子(VIF)脱颖而出,成为识别和量化多重共线性影响的实用器具。通过操办每个自变量的VIF值,咱们大要细目导致多重共线性的特征,并遴荐相应的要领,以确保模子的隆重性和可证实性。

总的来说,允洽地措置多重共线性不错提升模子的性能,增强效用的可证实性,并确保咱们的展望成立在牢固可靠的统统揣度之上。通过有计谋地诓骗这些方法,咱们大要构建出不仅准确,而况愈加可靠和易于分解的模子。